関数列の収束：n大でどういう関数に近づくか．2種類


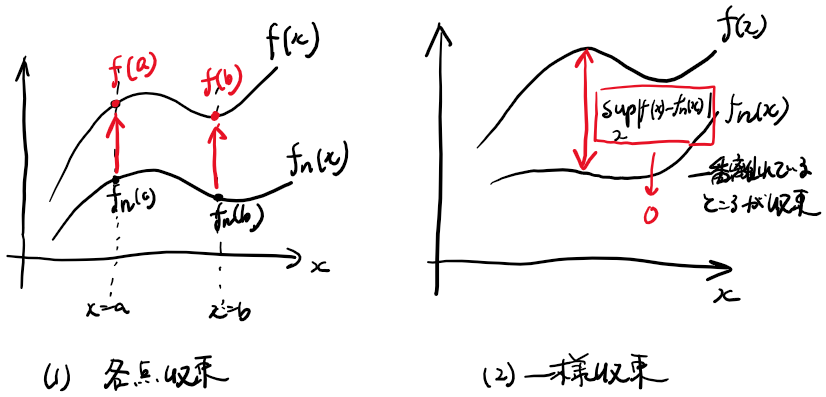
各点収束（各点において収束）

定義

区間内の任意の点$a$において、
\displaystyle \lim_{n\to\infty} f_n(a)=f(a)
が成り立つとき、$f_n(x)$は$f(x)$に各点収束するという

説明

xの値を固定すれば、$f_1(a),f_2(a),\dots$という数列の極限として考えられる。この数列が$f(a)$に収束することを主張している。おおまかにはどの点の関数値も収束するということ。

一様収束（xに対して一様に収束）

定義

区間内の任意の点$a$において、
\displaystyle \lim_{n\to\infty} \sup_x |f_n(x) - f(x)| = 0
が成り立つとき、$f_n(x)$は$f(x)$に一様収束するという

あるいは

$\forall \epsilon \ge 0$に対して、$x$によらないあるNが存在して、すべての$x$とすべての$n \geq N$に対して、$| f_n(x) - f(x)| \le \epsilon$が成立。
を定義としても良い（こちらの定義のほうが、一様とは$N$が$x$によらず$x \in X$に対して一様にとれることの意ということが分かりやすい）

説明

f:id:karate_odori:20190923215322p:plain
各点収束と一様収束

理論例

1. $[0,1]$で定義された関数列$f_n(x) = \frac{x}{n}$は$f(x) = 0$に一様収束する。

($\because$)
$| f_n(x) - f(x)| = \frac{x}{n} (\because 0 \leq x \leq 1)$より
$\sup_{x} |f_n(x) - f(x)| = \frac{1}{n} \rightarrow 0 \ (n \rightarrow \infty)$
あるいは、まず$\epsilon \ge 0$を固定する。
$| f_n(x) - f(x) | = \frac{x}{n} \leq \frac{1}{n}$(xに非依存)
$N \geq \frac{1}{\epsilon}$ととることで、$\forall n \geq N$について
$\frac{1}{n} \le \epsilon$より$|f_n(x) - f(x)| \le \epsilon$としてもよい

2. $[0,1]$で定義された関数列$f_n(x) = x^n$は各点収束するが、一様収束しない。

($\because$)
\displaystyle f(x) = \begin{cases} 1 \ (x = 1) \\ 0 \ (otherwise) \end{cases}
に各点収束することは明らか。
$| f_n(x) - f(x) | = | x^n| \le \epsilon$
$\Leftrightarrow n \ge \frac{\log \epsilon}{\log x}$となり、$x$が1に近いといくらでも大きくなって、$N$がとれないので一様収束しない。